이진법과 2의 보수
이진법이란?
이진법은 무엇인가? 아니 그 전에 십진법에 대해서 알아본다.
십진법은 누구나 알고 있는 진법이다.
십진법이라고 가르쳐주지 않아서 헷갈릴 뿐이다.
십진법은 수를 아래와 같이 손으로 세는 것과 같다.
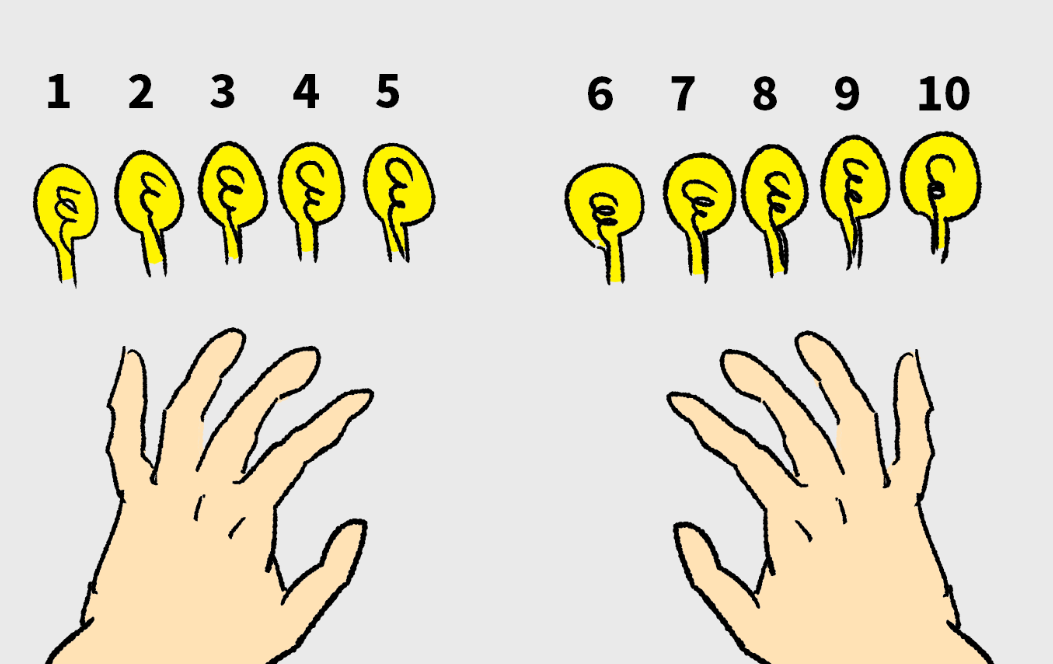
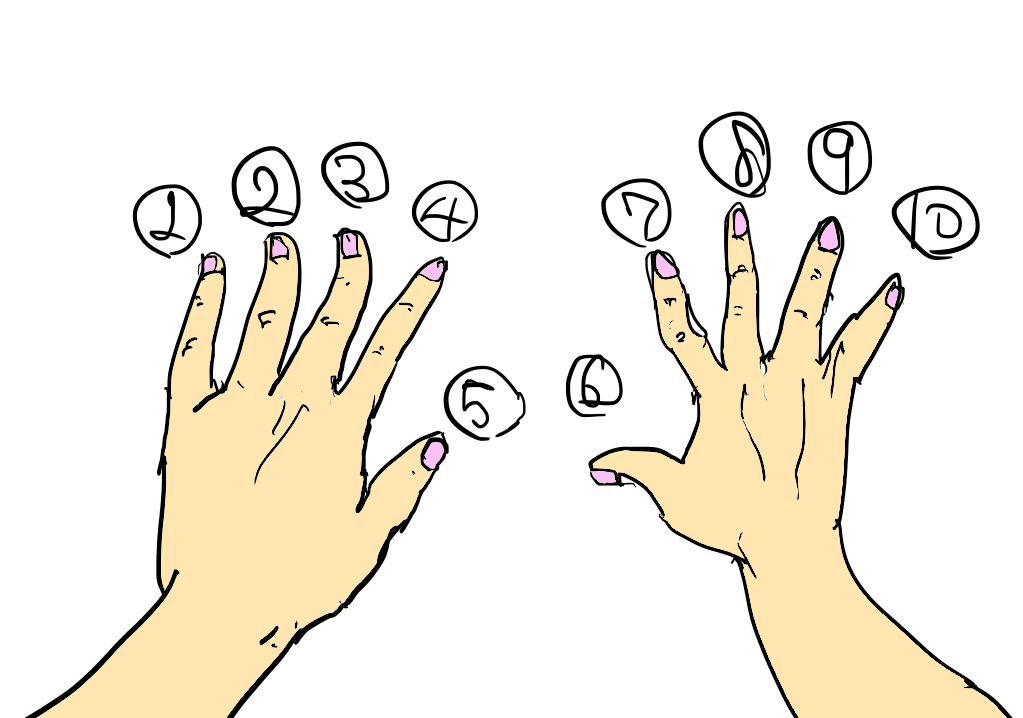
왼손 새끼손가락부터 오른속 새끼손가락까지 1부터 10까지 간다.
10은 실제로는 0이 하나의 자리수(digit)를 표현하는 것에 불과하다.
10진법 이하
10진법이라면 0부터 9까지 수를 사용한다는 뜻이다.
- 9진법이라면 0부터 8까지
- 8진법이라면 0부터 7까지
...
- 2진법은 0과1을 사용하고
- 1진법은 0?
1진법은 기호 하나만 쓰기 때문에 자리수(digit)개념이 없다.
1진법을 나타내려면 0 0 0 0 0 (10진수 5)
이렇게 원초적으로 점을 찍어 표현해야 한다.
컴퓨터는 0과1의 이진법을 사용한다.
이진법을 손으로 표현하면 아래와 같다.

손가락 두개 1과 10 이다.
1과 2가 아니라 1과 0인 점에 주의한다.
컴퓨터에서 0과1이라고 말하는데 일반 수의 개념하고 다르다.
컴퓨터의 0은 트랜지스터에 전류가 흐르지 않는 상태고
1은 전류가 흐르고 있는 상태이다.
즉 두개가 실체가 있다.
이것을 기계적으로 구현할 수 있으면
딱히 전자가 아니라도 컴퓨터를 만들 수 있다고 한다.
(아래 참고 문서에 유튜브 영상에서는
나무로 만든 기계로 튜링머신을 만들었다)
그런데 인간의 0 개념은 실체가 없다.
손가락으로 0의 상태가 표현이 안된다.
이 차이가 컴퓨터에서 0을 보는 시각이 달라지게 만든다.
컴퓨터에서는 16진수 0x0000이란 메모리 주소를 만들 수 있다.
0x0000이라는 메모리 저장소도 실제 존재한다.
컴퓨터는 0과 1을 인간의 손가락 처럼 올렸다 내린다.
컴퓨터는 Zero Based Index 를 채택해서 숫자가 0부터 시작한다.
즉 하나가 0 둘은 1을 사용한다.
인간은 0은 다른 목적으로 남겨두고
1부터 사용한다. 하나가 1 둘이 10이다.
요차이가 컴퓨터의 세계에 들어와서
알게되는 첫번째 인간과 기계의 차이점이다.
기계에겐 0이란 것 조차 세야하는 대상이고
인간은 세지 않고 0을 관념적으로 파악할 수 있다.
0은 생각보다 어려운 개념으로
인류가 0을 발견한 것은 그리 오래되지 않았다.
컴퓨터는 0이란 공간을 사용하고 있음에 주의한다.
중학수학 | 0이란 무엇인가? | 0의 리뷰
0은 무엇인가? 수의 세계에서 0은 특별한 위치를 갖고 있습니다. 현대인은 0의 개념을 무리없이 받아들이지만 0이 발견된 것은 5세기경 인도에서 사용하기 시작했다고 합니다. 그러니까 그 전에 0
digiconfactory.tistory.com
콩으로 표현 이진법
이진법 (二進法, binary) 두개가 되면 다음 자리수로 간다.
(앞으로 전진 할때의 진이다.)
마찬가지로 십진법은 열개가 되면 다음 자리수로 간다.
이진법을 콩으로 세어 보면 아래와 같다.
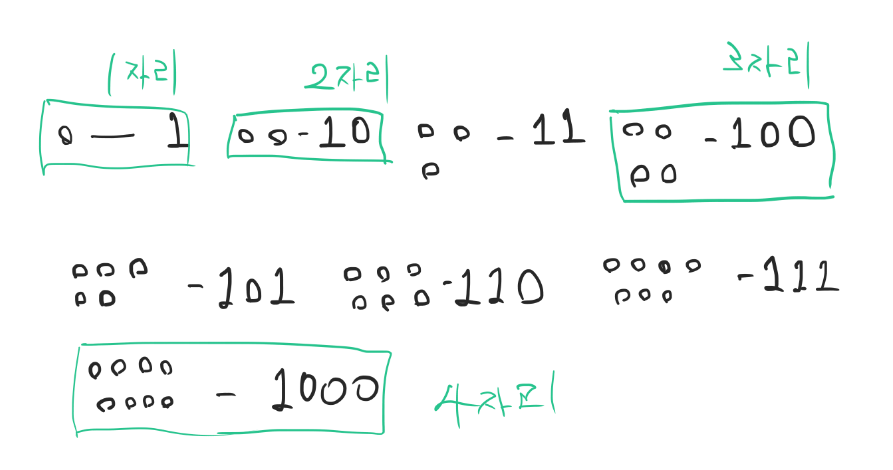
자리수가 1자리에서 2자리로 바뀔때 두배가 되고,
3자리로 바뀔때 2자리의 두배가 되고,
4자리로 바뀔때 3자리의 두배가 된다.
누구나 이해할 수 있을 정도로 간단하지만
이진법은 세상을 바꿀 정도로 강력한 원리이다.
현대의 컴퓨터는 이진법이기 때문이다.
(양자컴퓨터가 나오면 바뀔 수 있다고 한다)
적어도 21세기는 0과1 만으로도 이 세상의 모든 개념을
표현할 수 있다고 믿는 세상이다.
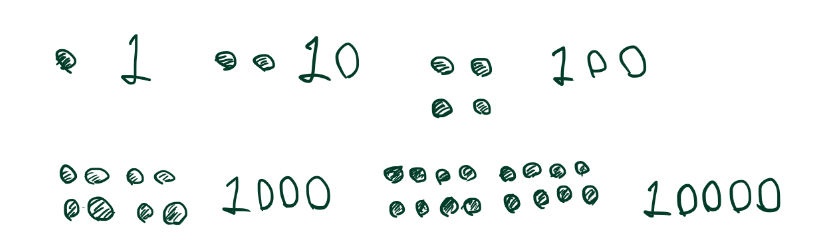
이진법의 원리는 모든 진법에 적용된다.
2진법 3진법 1000진법도 만들 수 있다.
그런데 실용적인 것들은 거의 정해져 있다.
일상생활에서는 시간의 12진법 분초의 60진법을 쓰고 있다.
초등학교 때 시간개념을 배우는데
조금 더 시간이 걸리는 사람들이 있다.
그것은 당연한 것으로 진법이 다름을
체감하면서 다른 수의 체계를 구분하기 때문이다.

60진법에서는 30분이 반이다.
12진법에서는 6시간이 반이다.
12진법은 또 24시간의 반이다.
정보기술의 시대인 현재에는
컴퓨터가 정말 이해할 수 있는 숫자가
1과0 뿐이라는 것이 어느정도 알려진 듯 하다.
좀더 정확히는 0과1로만 연산이 가능하고
무한에 가까운 표현이 가능한 것이 컴퓨터이다.
하지만 0과1로 할 수 있는 연산은 꽤 다양하다.
부울대수(Boolean Algebra)를 사용하여
만든 논리회로에서 연산한 결과들이
숫자, 이미지, 텍스트, 오디오, 비디오,
VR 가상현실 세계까지 표현할 수 있다.
그럼 VR까지가 끝일까?
컴퓨터의 가능성은 우리가 한계를 정할 수 없다.
왜냐하면 아직 잘 모르기 때문이다.
향후 양자컴퓨터가 상용화되면
인간이 어떤 세상에 살게될지 가늠이 되지 않는다.
컴퓨터의 표현 범위
컴퓨터에서 숫자를 Byte로 구성하면
00000000 부터
11111111 까지
표현이 가능하고 이는 1바이트(2의8승) = 256개 (0부터 255까지)의 범위가 표현이 가능하다.
1바이트는 8비트이다.
1비트가 0과 1로 이루어진 하나의 자리(digit)이다.
이는 컴퓨터적인 사고를 이해하기 위해
머리속에 항상 탑재되어 있어야 하는 단위다.
16비트면 256 x 256 = 65536개 범위이고
32비트면 4,294,967,296 (약 42억개) 범위가 표현가능하다.
64비트면 2의64승 18,446,744,073,709,551,616개 (거의 20개 자리수)까지 표현이 가능하다.
64비트는 1844경이란 천문학적 숫자인데...
일반인들에게 경험적으로 전혀 와닿지도 않고
실제 컴퓨터 프로그래밍을 하다 보면
무슨 물리 시뮬레이션을 할 때나 사용할 법한 단위이다.
32비트는 42억이라서 이 정도는 그래도 사용할 만한데
64비트와 32비트의 간격이 어마어마하기 때문에
가정에서라면 당분간 64비트를 넘는 CPU를 쓸일은 없을 듯하다.
현재 보통의 PC는 32비트 단위 처리가 가장 효율적이라고 해서
자바의 경우 기본 정수형은 32비트 int형이다.
32비트 int (정수)형은 숫자를 처리하는 하나의 기본 저장 공간에
약 42억개 범위 숫자를 저장할 수 있다는 말이다.
숫자라고 하지만 문자 인코딩을 하건
이미지 좌표 등 여러가지를 대응시킬 수 있기 때문에
문자 42억개, 픽셀 42억개 같은 것이 표현 가능하다.
과거 컴퓨터 홍보 문구에서 사용했던
16비트 칼라 24비트 칼라 같은 것은
컴퓨터의 이미지 표현력을 선전하던 것 이었다.
지금은 컴퓨터 장치의 디스플레이 성능이
너무나 좋아져서 천연색같은 표현은 장점이 떨어져서
그런 표현은 올드한 광고가 되버렸다.
* 2의 보수 ( two's complement) 계산법
2의 보수는 처음에는 좀 까다롭다.
우선 보수를 하는 이유를 알아보자.
대부분 컴퓨터개론에서 이진법과 2의 보수를 함께 가르친다.
왜냐하면 컴퓨터는 가산기를 사용해서 덧셈과 뺄셈을 하기 때문이다.
즉 덧셈 하나로 뺄셈까지 한다.
간단한 이진수의 덧셈을 해보면,
0101 ... 5
+ 0111 ... 7
--------------
1100 ... 12
가 된다.
뺄셈의 기능을 덧셈으로 해결해야 한다. 여기서 2의 보수가 필요하다.
12에서 7을 빼보자.
1100 ... 12
- 0111 ... 7
-------------
0101 ... 5
사람은 이렇게 계산한다.
하지만 가산기(Adder)는 이런 계산을 못한다.
컴퓨터에 뺄셈의 기능을 만들수는 있으나
컴퓨터 회로의 설계자들은
가산기로 덧셈과 뺄셈 둘다 하도록 만들었다.
가산기로 뺄셈을 하는 방법은 2의 보수를 사용하는 것이다.
2의 보수는 비트를 반전 시킨 후 1을 더한다.
그 전에 부호비트란 것이 있다.
최상위비트라고 하는 왼쪽끝 비트가 0일때 + 1일때 - 이다.
8비트의 경우 -128 부터 127까지 범위 정수를 표현할 수 있다.
부호비트를 하나 쓰니까 7개의 나머지 비트가 표현가능한 범위는 2의7승이다. (128)
비트를 반전시키는 것은 1의 보수를 만들기 위해서이다.
보수란게 보충하는 수(영어로 complement)라는 의미로 십진법에서 보면
5의 10의 보수는 5
4의 10의 보수는 6 이다
더해서 10이 되는 수라고도 볼 수 있다.
8비트의 1의 보수는 비트를 반전(0을 1로 1을 0으로) 시키면 된다.
이때 아래처럼 한 자리만 보수로 바꿔주는게 아니라
8개의 자리를 모두 바꿔준다.
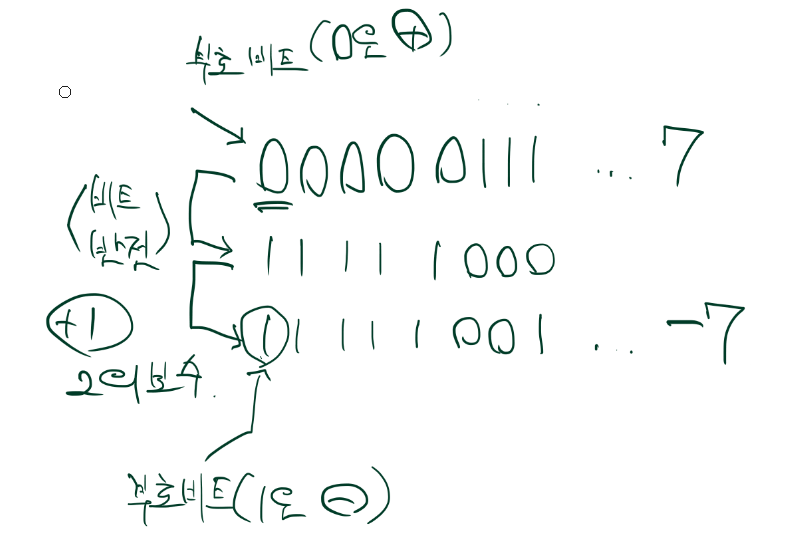
0의 1의 보수는 1이고
1의 1의 보수는 0이다.
가장 낮은 자리에 1을 더하면 2의 보수(음수)가 만들어진다.
이때는 모든 자리가 아니라 최하위비트(제일 낮은 자리)에만
1을 더해야 한다는 것을 잊지말자.
이유를 살펴보면 어떠한 양의 정수라도 비트를 반전시켜서 더하면...
* 2의 보수
0000 0001 (양수 1)
+ 1111 1110 (1의 보수) - 비트의 반전
-------------------------
1111 1111 (2의 보수 -1) - 음수로 부호가 변경된다
* 양수1과 2의 보수(음수)를 더하면
0000 0001 (양수 1)
+ 1111 1111 (음수 -1)
----------------------
1 0000 0000 (정수 0) - 자리올라간 1은 버려진다.
1111 1111 이 나온다. 여기 제일 낮은 비트에 1을 더하면
자리수가 넘어가면서 0000 0000 이 된다.
원래대로라면 1 0000 0000 이 되야 한다.
하지만 8 비트 범위를 벗어난 자리올림은 사라진다.
(8비트에 9비트 정보는 저장이 안된다)
즉 양수 0000 0001 의 1의 보수 1111 1110 을 더한 것에
0000 0001 을 더하면 0이 된다는 것은 1111 1111 이 -1 이라는 뜻이다.
즉 숫자를 더하다 보면 1, 10, 11, 100 와 같이
자리수가 늘어가는데 8비트라는 공간은
비트 8개만 저장이 가능하다.
8개 비트가 1로 꽉차있는데
여기다 1을 더하면 자리가 오를때
9번째 비트가 버려지므로 8비트는 0이 된다.
조금 어려울 수 있는데 비트를 위로 밀어내다가
위에 꼭지를 잘라버린다는 뜻이다.
이 Trick 을 사용하면 2의 보수에서
음수와 양수, 덧셈과 뺄셈까지 모두 표현이 가능하다.
아래의 표를 살펴보자. 2진수와 2의 보수를 가산(Adder)시키면 0이 된다.
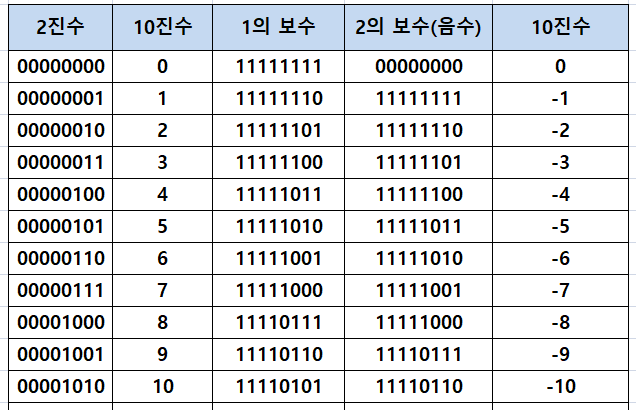
2의 보수는 백번 설명을 듣는 것 보다
직접 비트를 그려보는 것이 이해하기 쉽다.
참고문서 및 영상
아래는 영어 유튜브지만 내가 본 2의 보수 설명중에
가장 완벽한 설명 영상으로 추천드리니까 참고하시길 바란다.
10분안에 매우 깔끔한 설명을 한다.
https://www.youtube.com/watch?v=4qH4unVtJkE
컴퓨터 설계 개념과 소프트웨어가 영어로 쓰여지기 때문에
영문 그대로 이해하는게 제일 빠르다고 느낄 때가 많다.
한글 컨텐츠에도 위와 같은 멋진 설명영상이 많아 지길 바래본다.
아래 영상은 기계로 만든 튜링 머신이다.
튜링 머신은 폰노이만 구조 이전 초창기 컴퓨터 모델로
2차세계대전 중 독일군 암호해독에 쓰인 것으로 유명하다.
어느 외국 유튜버가 그걸 나무로 구현해냈다.
(정말 세상은 넓고 기상천외하다)
이걸 보면 지금과 같이 전자회로학이 발달하지 않았던
100년전에도 사람들 머리속에
컴퓨터 기계라는 아이디어는 지금과 크게 다르지 않았다.
Mechanical Turing Machine in Wood - YouTube
블록체인과 비트코인 탈중앙화 금융 시스템 (decentralized finance) | 블록체인 소개 영상 모음
블록체인과 비트코인 탈중앙화 금융 시스템 (decentralized finance) | 블록체인 소개 영상 모음
블록체인 비트코인 - 블록체인 기술의 하나 비트코인이 불과 몇개월만에 7000만원대를 넘어가면서 너도나도 비트코인에 뛰어들고 있습니다. 언론이 비트코인에 대해서 다루는 방식은 별로 진지
digiconfactory.tistory.com
알고리즘과 자료구조 입문
알고리즘 알고리즘에 대하여 일반인들에 회자된지는 조금 된 것 같다. 흔히 쓰는 '유튜브의 알고리즘에 의하여...' 의 알고리즘 말이다. 그런데 실제 컴퓨터 공학에 사용되는 알고리즘이란 무엇
digiconfactory.tistory.com
C언어 자료구조 - 배열의 구조
C의 대표적 자료 구조인 배열에 대하여 알아본다. 배열은 대부분의 언어에 기본으로 장착되어 있는 자료형태이다. 컴퓨터는 모든 데이터를 0과1의 이진 데이터의 형태로 저장한다. 이진법과 C의
digiconfactory.tistory.com





