이산수학 1 | 집합 (SETS) - 1

집합 (SETS)

집합은 이산수학에서 가장 기본적으로 연구할 대상이다. (그리고 수학 전체에서도)

이 포스팅은 이산수학의 개념을 알아본다.

일단 집합이란 말은 수학에서 쓰이지만 일상생활에서 많이 쓰이는 말이다. 그러니까 너무 어렵게 접근할 필요가 없다.

혹시나 참고가 될까해서 오랜만에 먼지 쌓인 수학의 정석책을 열어봤다. 역시나 어렵게 써있다. 그래서 예를 좀 바꿔본다.

우리 주변에서 흔히 볼 수 있는 집합의 첫번째 예는 '우리집 가족의 모임' 이다.

엄마, 아빠, 나 그리고 할머니, 할아버지, 여동생, 큰형 이 사람들은 전부다 유니크하고 순서가 없다.

약간의 기호를 넣어보면

가족 = { 엄마, 아빠, 나, 할머니, 할아버지, 오빠, 남동생 }

와 같다. 기호가 아니라 아이에게 그림을 그리라고 해도 이 정도 개념을 표현할 수 있을 것이다.

여기서 알 수 있는 것은...

-> 집합은 중복이 없고 순서가 없는 대상의 모임이다.

동생이 두명 있을 수 있지만 이름으로 부르면 다른 사람이고 나이는 있지만 정확한 순서는 없다. 엄마는 아빠보다 나이가 많을 수도 적을 수도 있다.

이산수학의 시작에서 집합(SETS)을 배우는 것은 딱딱 분리 된다는 것의 개념을 갖기 때문이다.

가족은 하나지만 구성원의 인생은 제각각이다. 엄마, 아빠가 결혼해서 잘 살지만 원래 처음부터 같이 살지는 않았고, 아이가 어릴 때는 엄마를 떨어지려고 하지 않다가 사춘기가 지나면 자기의 공간을 찾고 성인이 되면 독립한다. 집합의 각각 대상을 요소(element)라고 부르는데 각 요소들은 유니크하게 분리되어 있다.

*주: 요소(element)를 원소 또는 원이라고 정의하는데 용어가 많아지면 헷갈리니까 이 문서에서는 요소로 통일한다.

이것을 수에 대입하면 된다.

* 1부터 3까지의 자연수 -> 집합이다.

A = {1, 2, 3}

* 순서가 있는 듯 보이지만 상관없다.

A = {3, 2, 1}

도 같다.

일단 기호로 바꿨으면 읽을 줄 알아야 한다. 읽지 못하면 머리속에서 사라지기 쉽다.

쉽게 읽는 법이다.

* A는 집합이다. A는 요소 1, 2, 3을 포함한다.

익숙해지면 연결해서 읽는다.

* A는 요소 1, 2, 3을 포함하는 집합이다.

기호들

수학에 취미가 없다면 기호가 익숙하지 않을 수 있다. 그런데 수학은 기호를 읽지 못하면 의미가 없다. 천재들은 말도 안하고 눈앞에서 기호가 AR 디스플레이기 처럼 출력된다는데 대부분 평범한 사람은 그런 AR이 안나온다. 그러니까 기호부터 읽어야 한다.

∈ 은 소속에 대한 기호다. 영어로 is in 혹은 is an element of -> ...의 안에 있다. ...의 요소이다. 라고 한다.

1 ∈ { 1, 2, 3 }

-> 1은 집합 {1, 2, 3} 안에 있다.

-> 1은 집합 {1, 2, 3}의 한 요소이다.

∈에 빗금을 친 경우 반대이다.

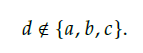
-> d는 집합 {a, b, c} 의 한 요소가 아니다.

한편 이 문장은 참이다. true statement

statement는 그냥 문장이 아니라 참이나 거짓이 될 수 있는 문장을 말한다. 그냥 내 의견을 말하거나 감상을 말하는 것은 statement 가 아니라는 부분에는 주의한다. 말이라고 다 같은 말이 아니다 -> 수학에 해당한다. 수학은 수학에서 사용하는 문장만 사용해야 한다. 그렇다고 외계어는 아니고 일상의 언어를 약간 검증하는 과정이 필요할 뿐이니 걱정할 필요 없다.

집합의 요소가 무한한 경우. 당연히 있다. 숫자도 그렇지만 인간도 무한한 존재이다. 현재 전세계 인구가 80억명 가까이 살고 있다. 만약 인간이 우주속에서 끝까지 살아남는다면 무한한 번식을 해서 전 은하계에 살게되는 날이 오지 않을까? 라고 상상을 해보면 그것도 무한의 집합이다. 우리가 알고 있는 것 처럼 완전히 똑같은 사람은 존재하지 않으니까. 사람은 유니크하다고 배웠다. 그렇게 알고 있는 것인지는 모르겠으나 어쨋든 인간의 집합도 무한대가 될 수 있다.

우주 자체도 무한대에 가깝다고 한다. 빅뱅으로부터 생겨난 우주의 물질들을 세어보는 것도 하나의 집합이 될 수 있다.

그런 상상이 어려우면 바닷속의 미생물을 상상해보는 것도 좋다. 미생물도 생물이니까 중복은 없을 것이고 순서도 없다. 요컨데 무한의 집합은 상상력이 중요하다. 대상이 무엇이든 간에.

문제는 이런 것들을 수학의 기호로 표현할 수 있어야 하는데 예를 들어 자연수의 집합을 표현해보자.

Natural Number = {1, 2, 3, 4, 5, 6, ,7 이렇게 쓰다보면...? 끝이 없다. 무한대다. 그래서

Natural Number = {1, 2, 3, 4, 5, 6, ,7, ... } 이렇게 표기도 하고

Natural Number = { x : x 는 자연수 }

이렇게 쓰기도 한다. : 콜론이 들어간 내용은 조건식을 말한다. x가 자연수이면 x이다.라는 뜻이다. x가 음수나 0, 실수면 안된다는 말이다.

이러한 형식도 형식이지만 중요한 것은 기호를 사용하여 수학적 진리를 나타내는 것이다.

그리고 저 수학의 기호를 보면서 무슨 생각을 하느냐가 중요하다.

자연수는 무한이라는데 무한은 셀수 있을까? 지금까지 세상에서 가장 많이 센 자연수는 무엇일까? 이런 질문들이다.

집합의 기호는 이보다 많은데 조급하지 말고 하나씩 배우면 된다.

기호를 연습하기

간단한 연습을 해보자. 다음을 읽어보고 요소를 나열해본다.

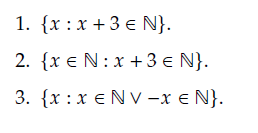
1. (x+3) ∈ N 으로 봐야한다.

-> x는 자연수보다 3이 작은 모든 수의 집합이다. N = { 0, 1, 2, ,3 ... } 이므로

요소를 나열하면 {-3, -2, -1, 0, 1, ... } 이다.

2. 이것은 무한의 특성이 들어있는 재미있는 집합이다.

-> x는 자연수보다 3이 작은 모든 수의 집합이다. 그리고 이 조건을 만족하는 수 중에서 자연수만 해당한다.

요소를 나열하면 {0, 1, 2, 3, ... } 으로 이것도 자연수다. 자연수보다 3이 작은 모든 수인데 여기서 다시 자연수를 골라내버리니까 다시 자연수로 돌아왔다. (약간 움찔했다.) 무한의 자연수에서 우리는 앞쪽은 셀 수 있지만 뒤쪽인 무한대쪽은 셀수가 없다. 1번 답인 {-3, -2 , -1 ... } 집합에서 -3, -2 , -1 이 세개의 숫자를 뺀 것이다. 앞쪽에서 보면 더 큰 집합도 무한대로 가면 뒤쪽은 보이질 않는다. 이걸 -3, -2, -1 이 있으니까 더 크다고 해야하나? 고민하게 만드는 집합이다.

3. 가운데 합집합 표시가 있다. ∨ 약간 다르긴 한데 컴퓨터의 기호가 약간 수학기호와 다른 경우라 그렇다.

x가 자연수에 속하고 그리고 x가 자연수에 마이너스 부호를 붙인 것에 속한 것은... -> 정수이다. 여기서는 -x에 0을 포함한 것으로 본다. 정수의 기호는 Z 이다.

* 참고자료 - 링크

Discrete Mathematics - An Open Introduction (openmathbooks.org)

CC BY-SA 4.0