대수 기초 | A FIRST BOOK IN ALGEBRA - 3 | 연산의 표현방식 (덧셈과 뺄셈)

- 연산의 표현 방식 덧셈
y + y + y + ... y를 7번 쓰면 7y 다
m + m + m + ... m을 x번 쓰면 xm 다
7이나 x를 coefficient 코이피션트 (계수)라고 읽는다.
coefficient는 숫자가 더해지는 횟수를 나타내는 수이다.
coefficient 가 없으면 1로 받아들인다.
6a, 2y, 25n, ax, 11xy 등의 예시로 분류해본다.

3. 존이 유리구슬 x 개 있다. 형제가 그에게 5개를 줬다. 그는 유리구슬이 몇개있는가?
-> xm + 5m
4. 매리에게 인형이 x개 있다. 어머니가 인형 y개를 준다. 몇개인가?
-> xd + yd
* 이번은 계수(coefficient)에 대한 내용이 나왔다. 또 이전까지는 미지의 수 즉 대수를 x 하나만 놓았는데 이번에서 부터는 x,y처럼 여러개의 대수가 나온다.
연습문제를 좀 더 풀어보자.
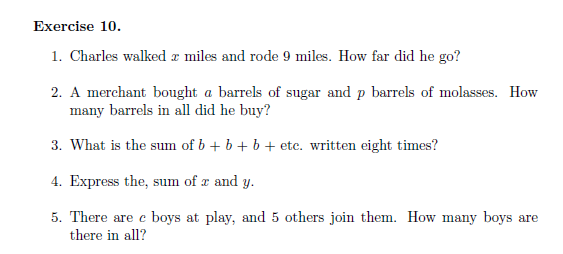
1. 찰스는 x마일을 걷고 9마일을 달렸다(아마도 자전거로) 얼마나 갔는가?
x 마일 + 9 마일
xm + 9m
(x+9)m
(x+9) 마일 갔다.
x+9을 계수로 했다. m 은 mile로 동일한 단위니까 x+9를 이을 수 있다.
2. 상인이 1 배럴의 설탕과 p 배럴의 당밀을 샀다. 그가 산 배럴의 총량은?
-> 배럴이 뭔지 모르면 헷갈린다. 배럴은 서양인들이 쓰던 나무 저장통이다.
농경문화가 발달한 한국에서는 장독대를 썼지만 무역이 발달한 서양에서는 이런 배럴을 들고 항해를 했다고 한다. 중간 부분이 커브가 진 것은 장독대나 배럴이나 비슷하다.
물론 요새 나무를 쓰는 곳이 있을까 싶은데 영어 사전의 정의를 보면 나무, 금속, 플라스틱으로 만든다고 한다.
위스키같은 술의 경우 현재도 오크 나무 배럴에 저장하는 것으로 알려져 있다.

이 문제는 설탕과 당밀이라는게 나온다. (밀의 종류인듯)
배럴의 양을 묻는 것이므로
(1+p) 배럴이 된다.
3. b + b + b ... 해서 b를 8번 쓰면?
-> 8b 라고 표기한다
4. x와 y의 합을 표시해보라.
x + y
5. c명의 아이들이 놀고 있다. 5명이 참여한다. 몇명의 아이들인가?
(c + 5) 아이

14. 상인이 밀가루 x 배럴을 첫주에 팔고, 40 배럴을 그 다음주에 a 배럴을 그 다음주에 팔았다. 몇개 팔았나?
( x + 40 + a ) 배럴
15. 두 숫자의 합이 74이다. 두 숫자의 차이는 18이다.
x = 큰수
x - 18 = 작은수
x + x - 18 = 74
2x = 92
x = 46
x -18 = 28
28과 46이다.
* 대수의 덧셈 표현에 관한 내용이었다. x를 여러번 쓰면 mx 같이 나타낼 수 있다는 부분 그리고 연습문제를 통해서 여러가지 구체적 추상적 문제에 대한 풀이를 볼 수 있다.
- 연산의 표현 방식 뺄셈

뺄셈에 관한 이론이다.
1 - 한 남자가 말을 225달러에 팔아서 75달러를 얻었다. 말은 얼마인가? (비용)
-> 225 - x = 75
x = 150 달러
2 - 농부가 양을 m 달러에 팔아 y달러를 얻었다. 양의 비용은?
m - y 달러가 양의 비용이다.
* 1,2번은 똑같은 형식인데 대수만 다를 뿐이다.
뺄셈은 마이너스 사인으로 표현한다.
3 - 한 남자가 특정 지점에서 출발해 북으로 15마일 남으로 30마일 , 다시 북으로 20마일, 북으로 5마일 남으로 6마일 여행했다. 그는 시작한 곳으로부터 어느 방향으로 얼마나 떨어져 있는가?
-> 북을 + 남을 - 로 놓고 본다.
+15 -30 +20 +5 -6
40 - 36 = + 4
시작 지점으로부터 북으로 4마일 떨어져 있다.
4 - 한 남자가 특정 지점에서 출발해 동으로 x마일 서로 b마일 동으로 m 마일 동으로 y마일 서로 z 마일 여행했다. 시작 지점에서 이동한 거리와 방향은??
동을 + 서를 - 로 놓고 본다.
+ x - b + m + y - z 마일이다.
* 1번부터 4번 문제를 놓고 보면 특히 4번 문제가 어렵게 느껴진다. 왜냐하면 x,b,m,y, z 이런 것들이 무슨의미인지 알 수가 없기 때문이다. 얼마나 큰 수인지 방향이 다른지도 모른다. 비단 동서남북의 문제뿐만 아니라 오른쪽 왼쪽 위와 아래, 과거와 미래, 이익과 손실 등 반대의 관계를 가진 모든 것들에 대해서도 적용될 수 있다. 반대의 관계를 가진 것들은 숫자의 표현에서 반드시 표현되야 한다.
대수에서는 0을 사이에 두고 양수(positive number)와 음수(negative number)로 나눈다. 숫자앞에 마이너스가 있다면 반대 방향으로 작용한다.
특정 지점에서 동서남북으로 수의 관계를 규정할 수 있다는 것이다. 동쪽을 + 서쪽을 - 북쪽을 + 남쪽을 - 로 정하는 것이 데카르트 좌표계이다. 그런데 꼭 이렇게 규정할 필요는 없다.
데카르트 좌표계 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 다른 뜻에 대해서는 직교 좌표 문서를 참조하십시오. 데카르트 좌표계(영어: Cartesian coordinate system)는 임의의 차원의 유클리드 공간(혹은 좀 더 일반적으로 내적
ko.wikipedia.org
일례로 파이게임에서는 꼭대기에서 우하향하는 좌표계도 있다. 여기서는 특정 지점은 0에서 시작하고 마이너스로 가지 않는다. (스크린 버퍼로는 사용할 수는 있다)

en:pygame:step003 [The Python Game Book]
thepythongamebook.com
음수는 대수학이 산수와 달라지는 부분이다.
1,2,3... 같은 숫자는 그 자체로 양수의 속성을 지니게 된다. 어떤 대상이 존재하는 것을 파악할 수 있는 것이다.
양 한마리 두마리 세마리...
고대인들은 수를 가지고 이렇게 세었을 것이다.
그런데 고대인들에게 -1 이 존재했을까?
확실히 양 -1 마이너스 1마리라고 하면 혼란스러울 것이다. -1 마리라는 양은 실제하지 않는다.
그러나 관계에서 규정하면 양 세마리가 있었는데 한마리를 팔았다라고 할때 -1 마리라는 말은 통하게 된다.
혹은 양 세마리 중에서 한마리거 늑대에게 잡혀갔다고 할 때도 -1 마리가 된다.
그들이 마이너스 1마리를 인지하지 못하더라도 하나가 사라지면 둘이 남는다는 것은 당연히 알았다.
0이라는 것을 발명한 후에 이런 개념을 좀더 다양하게 확장해서 사용할 수 있을 것이다.
양이 한마리가 없어도 이웃에가서 10마리를 빌려오면 나는 + 10 마리를 가지고 있지만 이웃에게 빌린 것이니까 - 10마리라고도 할 수 있다. 0을 설정할 수 있는 곳에는 어디에나 -와 +로 관계를 설정할 수 있다.
마이너스라는 개념을 도입하면 플러스 개념도 바뀐다.
기존까지는 양적인 수로만 봤다면 방향성도 볼 수 있게 되었다.
돈을 잃는 것을 마이너스로 표현하면 돈을 버는 것을 플러스로 표현할 수 있다. 0을 중심으로 확실한 방향성이 생겨난 것이다.
산수에서는 특정한 값을 다룬다면 대수학에서는 미지의 수(정해지지 않은 수)를 다루는 것이다.
그러니까 산수보다 범위가 넓고 복잡한게 대수학이다.
* 이제 개념을 잡기 위해 연습문제들을 풀 차례이다.

7. 한 남자에게 4명의 딸이 있다.
각자는 다음 동생보다 3살이 많다.
x가 가장 나이 많은 딸을 표현한다.
다른 아이들을 표현해보라.
x = 큰딸(장녀)
x - 3 = 둘째 딸
x - 3 - 3 = 셋째 딸
x - 3 - 3 - 3 = 막내 딸

8. 농부가 a 마리 소를 b 달러 주고 샀다. c 달러에 팔았다. 얼마를 벌었는가?
c - b 달러이다
a 마리는 소의 마리수이고 전체를 b 달러에 샀다고 하니 혼동하면 안된다. 역시 영어 해석이 안되면 문제를 풀기가 어렵다.
a 마리를 개당 b 달러 주고 샀다면 이야기는 달라진다. 그런데 이 해석이 어느쪽인지 필자도 잘 모르겠다. 워낙 100년전 교재에 풀이도 없기 때문에... 여기서는 두 가지의 경우가 있다는 것만 기억한다. a 마리의 개당 b 달러라면 c - ab 가 맞다. 출제 의도가 헷갈리긴 한다.

5. 한 남자의 수입이 a 달러이다. 지출이 b 달러이다. 얼마나 남았는가?
수입 - 지출
a - b 달러
* 간단한 문제다. 정말 간단해 보이지만 현실에서 마이너스가 나면 모두가 어려워한다.

* 이번 뺄셈 문제는 아무래도 사고 파는 내용이 많다. 당시에도 경제 문제에 관심이 많았나 보다.
11. 집을 x 달러에 팔아서 75달러를 벌었다. 집은 얼마였는가?
x - 75 달러 (에 집을 샀음)
12. 마차를 m 달러에 팔아서 x달러 손해를 봤다. 마차의 가격은 얼마였는가?
* 여기서 마이너스 손해 문제가 나온다.
손해는 마이너스 부호를 붙여야 한다.
-> 마차의 원래 가격 = 판매가격 + 손해 혹은 이익 (손해일때 - 이익일 때 +)
원래가격 = m 달러 - x 달러
(m - x) 달러

9. 5보다 큰 x는 얼마나인가?
좌표로 보면 좋을 문제다. x는 무한개 존재하니까 몇개인지는 알 수가 없다. 산수로는 표현이 불가능한데 대수로는 표현이 가능하다.
x + 5
5 보다 커야 하니까 x에 5를 더한다. 이때 x는 0이 아니어야 하고 x는 양수여야 한다. (x > 0)
10. 두 숫자의 차이가 9이다.
숫자를 어떻게 표현할 것인가?
-> 어떻게 표현할 것인가라는 질문에 답이 있다.
큰수를 대수로 잡느냐 작은수를 대수로 잡느냐에 따라 달라진다
큰수를 잡으면
x = 큰 수
x - 9 = 작은 수
작은 수를 잡으면
작은수를 잡으면
x = 작은 수
x + 9 = 큰 수
큰수 작은수는 상대적인 것 임에 유의한다.

17. 한 투표에서 두 후보자에게 1065개가 투표했다. 승자는 207표 앞섰다. 각각 얼마나 받았는가?
x = 승자
x - 207 = 패자
x + x - 207 = 1065
2x = 1272
x = 636
x - 207 = 429
429, 636 표이다.
18. 상인이 m 달러로 연초를 시작했다.
첫달에 x달러 벌고 다음달에 y 달러 잃고 다음달에 b달러 벌고, 넷째달에 z 달러 잃었다. 마지막 달에 얼마나 가지고 있는가?
* 벌면 + 잃으면 - 다
m +x -y +b -z
이번 포스팅에서는 대수학의 표현방법 덧셈과 뺄셈의 튜토리얼 이었다.
수학을 잘하기 위해서는 국어(미국은 영어)를 잘해야 한다는 생각을 다시끔 하게되었다. 우리가 말귀를 못알아 듣는다는 말을 가끔 하는데 국어를 잘하지 못하고 수학을 잘하기는 힘들다. 말귀를 알아들어야 수학이 된다. 한편으로는 수학을 가르치는 교사들의 언어 능력도 더 중요해지는 것이다.
이것은 프로그래밍 언어를 배울 때도 같은 것 같다. 얼마나 말을 잘 하냐에 따라서 이해도에 큰 차이가 있다.
다음 포스팅에서는 곱셈의 표현 방법 부터 커버하게 될 것이다.





