대수기초 | 파이썬 수학 | A FIRST BOOK IN ALGEBRA - 9 | 연산자 다항식 곱셈
다항식 곱셈이다.
기본적으로 하나씩 다 곱해야 한다. 대수가 복잡해지면서 이 부분에서 좀 지루해지지 않나 싶다.

a - b + c
x
-----------
ax - bx + cx
처럼 (a - b + c)x 하나씩 다 곱해서 더해줘야 한다.
차수의 크기가 같다면 계수를 더한 후 대수를 붙이면 된다. 이를 테면 3x^2 + 4x^2의 경우 (3+4)x^2 가 된다.
simplify 주어진 다항식을 최대한 간결하게 하는 것이 목적이다.
*여기서 다항식과 단항식의 차이에 대하여 한번 짚고 넘어가면 좋을 듯 하다.
위키피디아 정의에 따르면 다음과 같다.
단항식(單項式, monomial)은 단 하나의 항만으로 이루어진 다항식이다. 그 하나의 항은 계수와 변수, 그리고 변수가 거듭제곱된 지수로 이루어진다. 5, 2x, 3xy2은 단항식의 예이다.
다항식(多項式, 문화어: 여러마디식, 영어: polynomial)은 단항식들의 덧셈과 뺄셈으로 이루어진 식이다. 예를 들어, x2 - 2x + 3, 4x3, 5xy + 6은 모두 다항식이다.
영어 교재를 참고한다면 monomial 이 단항식 polynomial 이 다항식이다.
단항식에는 더하기나 빼기가 없다.
단항식은 동일한 변수(x, y, z 같은)의 차수가 같고 곱셈으로만 표현이 된다. 그러나 다항식은 곱셈으로 표현이 안되는 것들을 덧셈과 뺄셈으로 표현해놓았다. 차수가 다르면 덧셈이 불가능하다. 때문에 차수가 다른 것들이 대수식에 포함된다면 다항식이다.
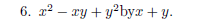
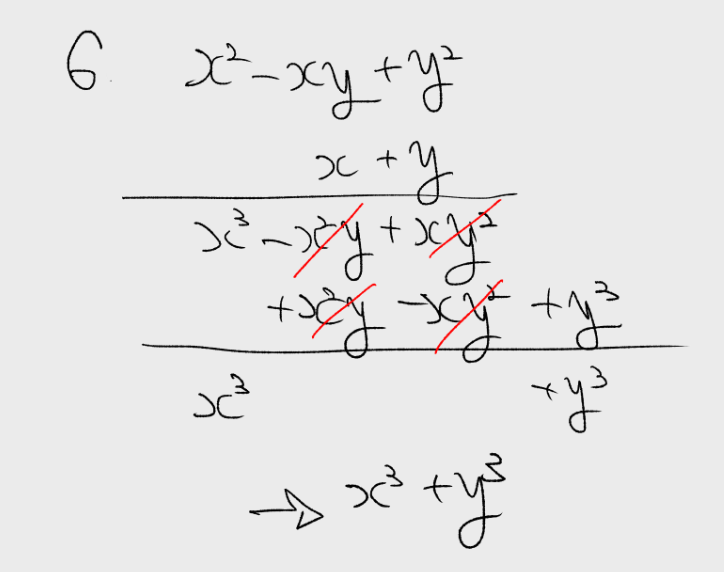
다항식의 곱셈풀이는 반복적인 부분이 많아 큰 재미가 없으니 좀 느긋한 마음으로 풀어야 한다.

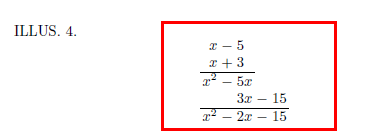
차수가 같은 두 다항식의 곱이다. 부호와 계수가 어떻게 바뀌는지 살펴보면 x^2 은 항상 같다. x에 부호가 없으니까.
부호에 따라 x는 부호도 다르고 계수는 두가지가 나온다. 마지막 상수는 값은 같지만 부호는 달라진다.
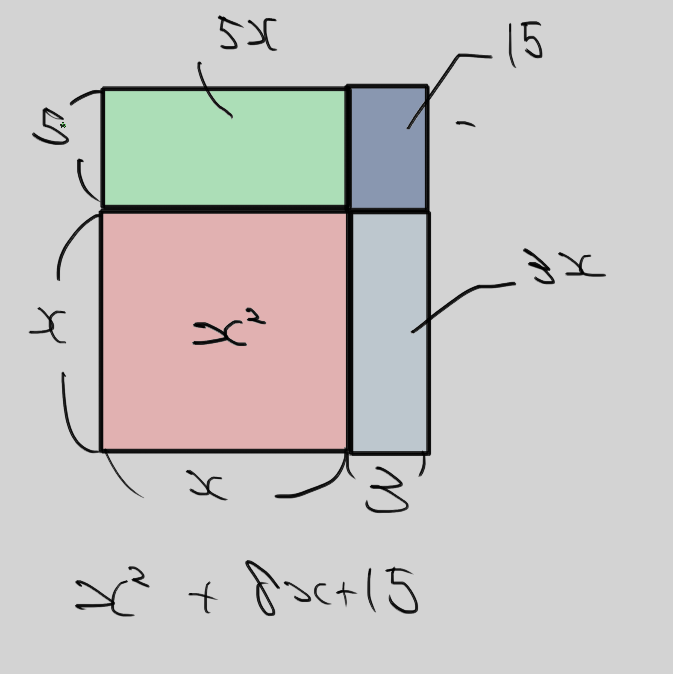
기하학으로 보면 좀더 시각적인 부분이 좋다.
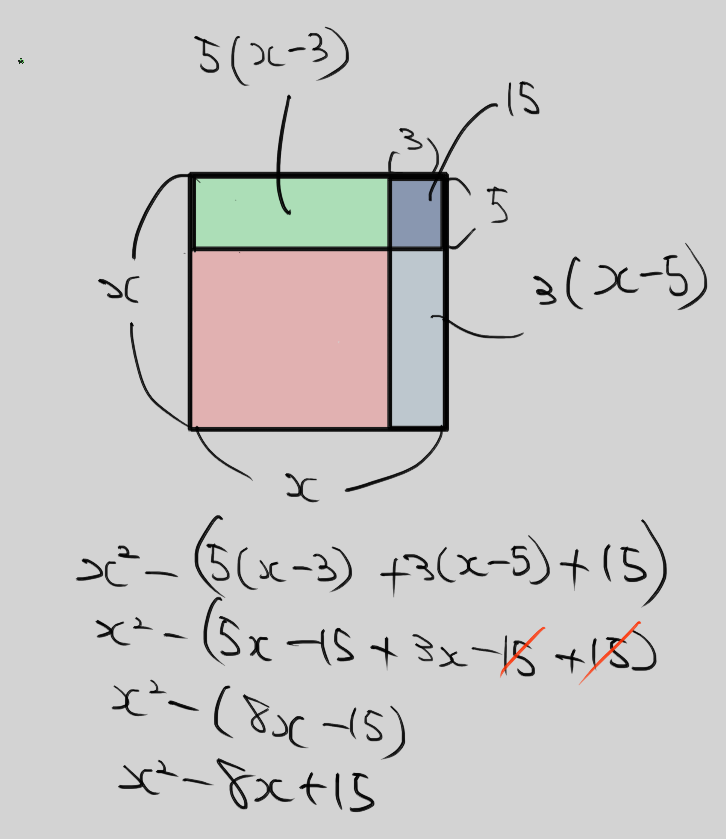
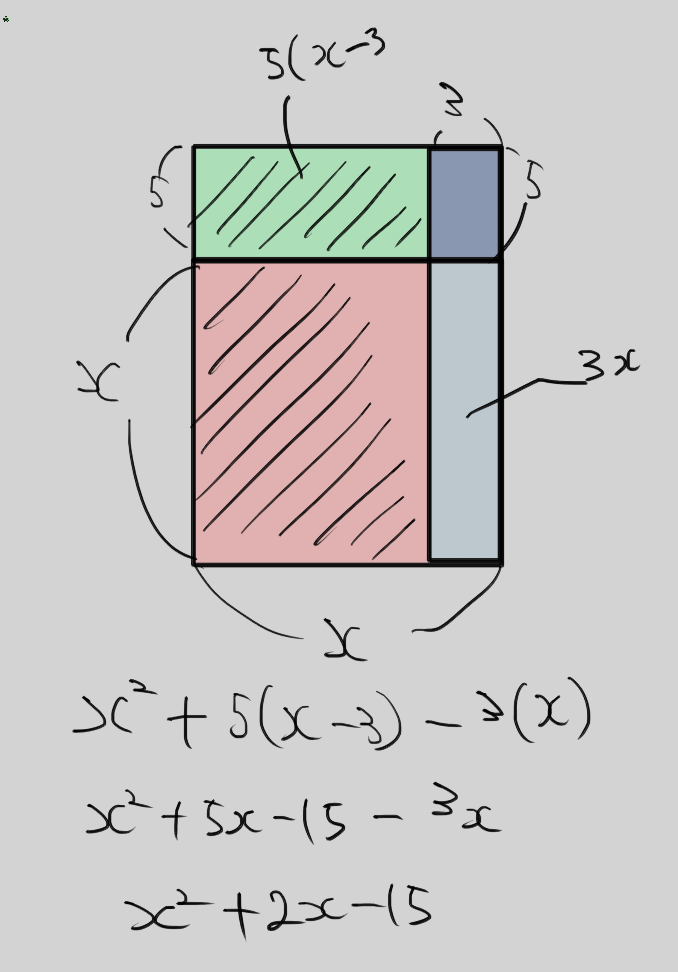
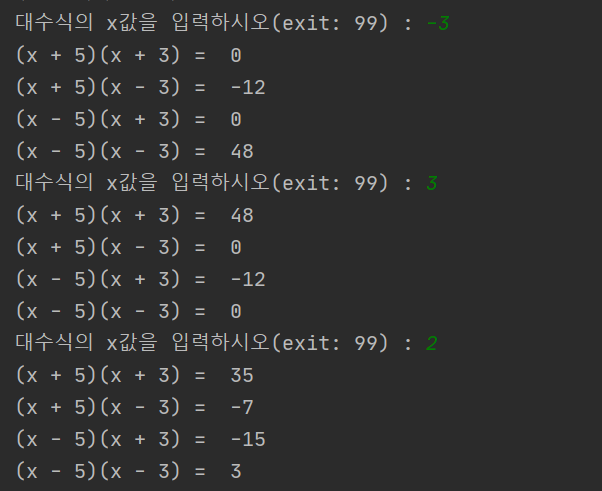
파이썬으로도 구현해본다.
x = 0
while True:
if x == 99: break
x = int(input('대수식의 x값을 입력하시오(exit: 99) : '))
print('(x + 5)(x + 3) = ', (x+5)*(x+3))
print('(x + 5)(x - 3) = ', (x+5)*(x-3))
print('(x - 5)(x + 3) = ', (x-5)*(x+3))
print('(x - 5)(x - 3) = ', (x-5)*(x-3))
다음은 지수의 곱셈이다.

x^2 에 ^3을 곱하면 x^6이 된다.
계수와 같이 있었다면
5x^3 에 ^2을 곱하면 25x^6이 된다. 지수와 계수에 대한 연산이 혼동스럽지만 실제 숫자로 계산해 보면 일치한다.
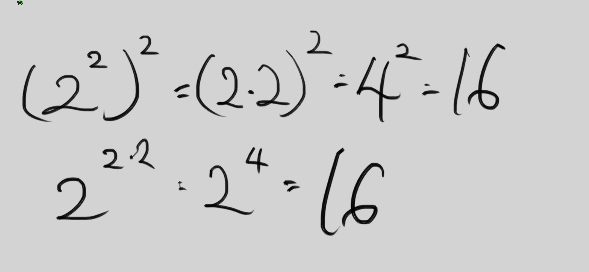
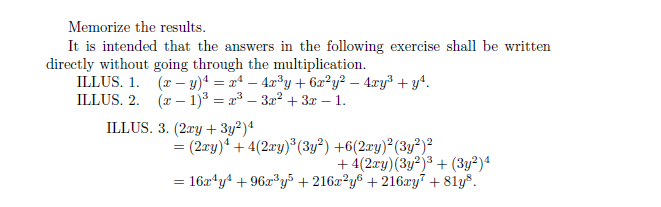
이 120년 전의 교재에서도 안타깝지만 3차와 4차 식의 경우 그냥 공식을 외우라고 나와있다. 수학공식을 암기하는 친구들이 역사적으로 오래되었다는 것은 좀 안타깝다. 물론 외우는 것은 필요한데... 위의 식은 부호가 달라지는 경우도 있으니까 쉽게 외워지지 않을 것 같다. 어쨋든 입시를 준비하는 학생에게는 의미가 있을 것 같다.
이 포스팅 시리즈의 목적은 암기같은 것이 아니기 때문에 이런 부분은 스킵한다. 그리고 사실 대수식의 차수가 올라갈 수록 많이 어려워지는 것은 당연한 것이니까 그렇게 고민할 필요는 없다.
다음 포스팅에서는 48페이지의 나눗셈(division) 에 관하여 다루도록 한다.





