대수기초 | 파이썬 수학 | A FIRST BOOK IN ALGEBRA - 6 | 연산자 덧셈
연산을 Operation 이라고 한다. 컴퓨터에서 연산할 때도 Operation 단어를 사용한다. + - 부호를 Operator 라고 하며 컴퓨터에서는 그 의미가 좀 더 확장되었다. < > 크기 비교 연산자 . 주소 연산자 등 파이썬만 해도 다양한 연산자를 지원하며 심지어 사용자 정의 연산자까지 만들 수 있다.
컴퓨터 언어 측면에서 연산자하고 함수하고는 조금 혼동이 있을 수 있다. 함수는 좀 더 많은 일을 수행하는 반면 연산자는 항을 가지고 연산한다.
뭐 이런 저런 것들에 대한 부분은 하다 보면 익숙해지는 부분이다.
컴퓨터에서의 연산자와 수학에서의 연산자가 의미가 같은 것도 있고 아닌 것도 있겠지만 결국 이 수들을 가지고 어떤 목적을 달성하려는 행위에서는 같다고 볼 수 있다.
이번 포스팅은 대수 연산이다
덧셈 ADDITION

위의 일러스트에서 보여주는 것은 같은 항끼리 묶어야 한다는 것이다. 계수는 계수끼리 같은 글자들(미지의 숫자를 대표하는)끼리 모여야 한다는 것이다.
3ax
5ax
2ax
와 같이 모으면 이 숫자에는 + 관계가 성립하므로 10ax 가 된다. 대수에서는 항상 부호관계가 존재한다.
+와 - 에서 음수 양수 둘은 항상 반대의 성질을 가진다.
식이 복잡하지만 결국 같은 것을 모으는 과정이다.
대수에서 나오는 용어들 term 항 , 다항식, 단항식 등은 차차 익숙해지게 될 것이다.
식의 정리이기 때문에 바로 연습문제로 들어간다.
* 연습문제 유형 15. 합계를 찾아라
[문제]
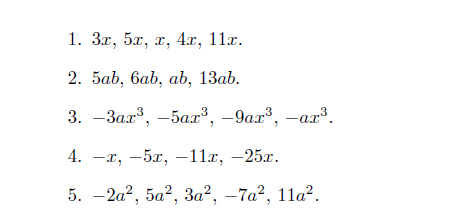
1.
->대수는 x 하나다. x를 하나의 길이라고 놓아도 되고 크기라고 생각해도 된다. 어떻게 생각하건 그건 대수를 생각하는 사람의 머리속에 있는 개념이다. 실제 세상에 x라는 것은 존재하지 않는다. 추상적인 개념일 뿐이다.
단 x가 무엇이든 간에 하나의 식에 사용될 때 x가 여러번 나오더라도 항상 같은 값이어야 한다. 바뀌면 x가 아니다. x에 1을 넣는다면 모든 식에 1을 넣어야 한다. 첫번째 x에는 1을 넣고 두번째 x에는 2를 넣으면 대수는 성립할 수 없다.
3x + 5x + x + 4x + 11x
앞의 숫자를 계수(coefficient) 라고 한다. 계수만 모아보자.
3 + 5 + 1 + 4 + 11
아무 표시없는 x의 계수는 1이다.
다 합쳐서 24이다.
24x 가 된다. 이렇게 되는 것은 덧셈과 곱셈의 원리이기 때문이다.
python 으로 구현해보자. 동일한 동작의 반복이니까 쉽다.
x = 1
while True:
x = int(input('x에 숫자를 넣으시오 (exit: 999) : '))
if x == 999:
break
result = (3 * x) + (5 * x) + (1 * x) + (4 * x) + (11 * x)
print('연습문제 1:', result)
print('종료합니다')
24x 는 24의 배수이다.
파이썬에서는 일일히 수식을 다 세워야한다. 위의 코드는 과정을 보여주기 위한 것이다. 실제로는
result = 24 * x
로 간단하게 끝날 일이다. 이렇게 하면 CPU도 일을 덜해서 효율적이다. 사람도 머리 많이 쓰면 안돌아가지만 컴퓨터도 마찬가지다. 같은 시간에 처리할 수 있는 한계가 있다. 그러므로 항상 식을 단순화 시키려고 한다.
2~5번은 부호를 주의해서 본다. 문자가 많아질 수록 헷갈리기 쉬워지는게 대수다.
4번 같은 경우 전부 음수다.
-x - 5x - 11x - 25x 이것을 방향성이라고 생각하면 좋다. 마이너스와 플러스는 반대 방향으로 힘이 작용한다. 전부 마이너스면 부호는 그대로 두고 계수만 더한다.
-1 -5 - 11 -25 = -42 이다. 수직선에서 음의 방향으로 쭉 더했다고 볼수있다.
-42x
x 그 자체는 부호가 플러스일수도 마이너스 일수도 있으니까 그대로 써주면 된다.
이 항의 뜻은 -42 배수 라는 것이다.
제곱이 들어간 3번과 5번 문제도 같은 방식으로 다루면 된다.
대수학의 문제를 푸는 것은 단순화한다는 말과도 같다. (simplify)

단순화 할 때도 같은 문자끼리 묶어주면 된다. 9번은 a^2 가 공통된다.
a^2(4-5-8-7)
-16a^2 로 단순화 시킨다. 다른 것들은 어렵지 않은데 10번의 경우 문자가 여러개 나와서 복잡해보인다.
이런 경우도 같은 것끼리 묶는다.
(1-2)x^5 +(5+3)a^4b+(10-7)ab
-x^5 + 8a^4b + 3ab
묶어지지 않는 것들은 따로 빼놓으면 된다.

13. 한 여성이 리본을 m 센트에, 테이프를 d 센트에, 실을 c 센트에 샀다.
x 센트를 청구서에 지불했다. 결제의 잔액은 얼마나 남았는가?
결제 안한 것 = 전체 청구액 - 현재 결제액
(m + d+ c ) 센트 = 전체 청구액
현재 결제액 = x 센트
(m + d + c) - x 가 청구서의 잔액이다.
* 리본이나 개별 제품들의 단위당 가격이 나와있지 않다. 이것은 센트(Cent) 자체를 단위로 모으는 것에 의미가 있다.

27. 남자에게 소가 x 마리 말이 y 마리 있다.
10마리의 소를 다른 사람의 말 19마리와 교환을 했다.
각각 몇마리 있는지 표현을 해보라.
* 교환이라는 것은 주고 받는 것이다.
소 10마리 = 주는 것
말 19마리 = 받는 것
소 x 마리 말 y 마리 = 처음 상태
*소 x - 10 마리
*말 y + 19 마리
파이썬으로 한번 구현해보자.
cow = 0
horse = 0
cow,horse = map(int, input('현재 소와 말의 값을 넣으세요.').split())
print('소: ',cow,'마리')
print('말: ',horse,'마리')
print('*소 10마리를 말 19마리와 교환합니다.')
cow = cow - 10
horse = horse + 19
print('소: ',cow,'마리')
print('말: ',horse,'마리')
코드로 구현하면 수학과는 좀 다르다는 것을 이해해야 한다. 수학은 개념을 가지고 하기 때문에 표현범위가 무한대에 가깝지만 컴퓨터안에서 구현하는 것은 제약사항이 많다.
항상 초기화를 시키는 이유는 안전하고, 문제 발생시 대응이 빨라지는 습관이기 때문이다.
코드에서 cow = cow - 10 이것은 등식이 성립한다는 표현이 아니다. cow 변수에 cow - 10 표현식의 결과값을 입력하겠다는 말이다. 왼쪽에 있는 변수에 할당시키는 것이다. 따라서 대수처럼 미지수를 남발할 수는 없다. 오른쪽에 있는 수가 미확정되면 프로그램은 예외를 발생시키며 종료된다.
그래서 데이터가 입력되는게 확인이 되야지 프로그램을 실행할 수 있다.
이것은 수학보다는 컴퓨터 프로그래밍의 영역이라 여기 정도만 설명한다. 궁굼한 사람은 파이썬 튜토리얼을 참고하길 바란다.
(파이썬이 쉽지만 숙달하는데 시간이 의외로 많이 걸린다)
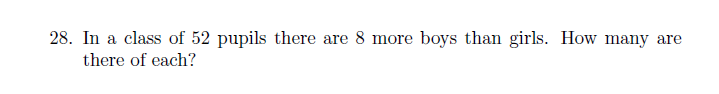
이 교재의 앞쪽에서 부터 계속 나온 질문이다. 복습이다.
클래스 한 반에 52명의 아동이 있다.
여자아이보다 남자아이가 8명 더 많다. 각각 얼마인가?
x = 여자아이
x + 8 = 남자아이
x + x + 8 = 52 전체 클래스
2x + 8 = 52
2x = 44
x = 22
x + 8 = 30
각각 22명, 30명이다.
girl = 0
total_pupil = 52
girl = int((total_pupil - 8)/2)
boy = girl + 8
print('여자아이 : {0}명\n남자아이 : {1}명\n총 : {2}명'.format(girl,boy,total_pupil))
대수의 식을 그대로 코딩할 수 없으니까 확실한 몇개의 정보를 가지고 일반성이 있게 만든다. 예를 들어서 숫자를 바꿔도 동작하게 만든다. 그게 변수를 사용하는 방식이다. 여러모로 변수와 대수는 공통점이 많다.

마지막으로 대수 연산에 있어서 가져봐야 할 의문들이다.
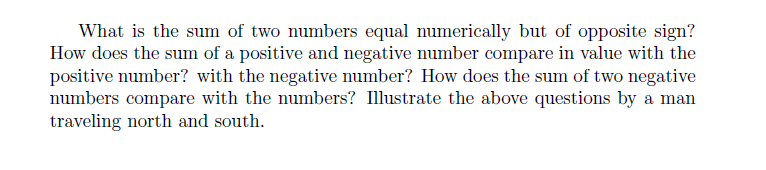
*두 수의 합은 얼마인가? 이 두수는 숫자적으로 같다. 그런데 부호가 다르다.
-> 합은 0이다. 산수에서도 5 = 5 이면 한쪽 부호가 -5 이다. +5와 합하면 0이 나온다.
대수에서는 x = x 일 때 x + (-x) = 0 이다.
*양수와 음수의 합은 값으로 어떻게 비교하는가? 양수일 때, 음수일 때?
*두 음수의 합을 숫자에 비교하면? 이 문제들을 북쪽과 남쪽으로 여행하는 사람에 빗대어 묘사하라.
-> 영문 해석이 좀 매끄럽지가 않은데 부호있는 숫자들의 합의 결과에 대한 이야기다.
예를 들어 양수와 음수를 더하면 반대방향으로 작용하니까...
+5와 -2 다. 3이다. 여기까진 괜찮다. 그런데...
+5 와 -7이다. 자연수 5에서 7을 뺄수는 없다. 이런 경우 수직선에 있다고 생각한다.(동서, 남북의 1차원 수직선이다)
북의 방향으로 가는 힘이 5만큼 들고, 남으로 가는 힘이 7이다. 서로 만나는 지점을 0이라 했을 때 남으로 2만큼 진행한다. 남의 방향으로 작용하는 힘에 대하여 음수라고 부른다.
계산을 하기 위해서는 어느쪽이던 큰 숫자가(큰 힘을 가진 쪽이) 항상 이기는 게임이니까 큰수에서 작은수를 빼고 방향성에 따라 부호를 붙이면 된다.
그림으로 보면 좀 더 이해가 빠르니까 말이 헷갈리면 아래의 포스팅을 참고한다.
(말로만 설명이 잘되는 사람이 그리 많지는 않다...)
수직선에서 덧셈과 뺄셈 | 숫자로 보는 인생
덧셈과 뺄셈은 누구나 기본은 한다고 생각한다. 초등학생도 그 정도는 할 수 있다. 그러나 덧셈과 뺄셈을 즐기기는 생각보다 어렵다고 한다. 학창시절 안좋은 기억 때문일 수도 있다. 지금 등교
digiconfactory.tistory.com
대수의 덧셈에 대하여 다루어 봤다. 대수는 그 자체가 곱셈의 속성을 가지고 태어난다. 그러니까 용어에 너무 얽매일 필요는 없다. 대한민국 국민이면 누구나 공교육에서 수많은 시간의 수업을 듣는다. 그런데 그렇게 쏟아온 시간이 비해서 수에 대하여 불편해한다.
이 블로그는 원리를 탐구를 하기 위한 공간이지 입시의 연장선이 아니다. 수학으로 철학을 하거나 프로그래밍 언어에 자유롭게 접목시키는 목적에 더 가깝다.
다음 포스팅에는 뺄셈 Subtraction 부터 알아본다.





